La optimización de la gestión de redes de riego a presión para reducir el consumo, coste energético y emisiones de CO2 es muy importante para poder conseguir un regadío sostenible. Con este post pretendo mostrar mediante un supuesto práctico, la gran repercusión que tiene en el consumo de energía de una impulsión, el manejo adecuado de la estación de bombeo.
Una comunidad de regantes dispone de la siguiente infraestructura para la reutilización del agua procedente de una EDAR con tratamiento terciario:
- Balsa de captación de unos 40.000 m3 de capacidad junto a la EDAR. El nivel mínimo de la lámina de agua está en la cota 80 m y el nivel máximo de la lámina de agua se da en la cota 83 m.
- Tubería de impulsión: 4.572 m de tubería PEHD DN 500 PN 10, y 1.428 m de tubería PEHD DN 500 PN 6.
- Estación de bombeo formada por cuatro grupos de bombeos (3+1) en paralelo, pueden funcionar simultáneamente 3 grupos y con 1 bomba de reserva activa. Dispone de un variador y tres arrancadores electrónicos. Las curvas de la bomba proporcionada por el fabricante son las siguientes: HB = 131+166·Q – 8546·Q2 (Q en m3/s y H en m.c.a.) h (%) = 2500·Q – 19500·Q2 (Q en m3/s)
- Balsa de regulación de unos 600.000 m3. La cota del nivel mínimo de la lámina de agua es 130 m y la de la máxima lámina de agua 140 m.
MES
|
m3/mes
|
m3/día
|
m3/semana
|
m3/h
|
Enero
|
142.891
|
4.609
|
32.266
|
425
|
Febrero
|
110.076
|
3.931
|
27.519
|
362
|
Marzo
|
172.834
|
5.575
|
43.209
|
569
|
Abril
|
152.861
|
5.095
|
38.215
|
503
|
Mayo
|
159.037
|
5.130
|
39.759
|
523
|
Junio
|
161.372
|
5.379
|
40.343
|
531
|
Julio
|
237.960
|
7.676
|
59.490
|
783
|
Agosto
|
271.519
|
8.759
|
67.880
|
893
|
Septiembre
|
162.640
|
5.421
|
40.660
|
535
|
Octubre
|
144.651
|
4.666
|
36.163
|
476
|
Noviembre
|
161.455
|
5.382
|
40.364
|
531
|
Diciembre
|
122.704
|
3.958
|
30.676
|
404
|
TOTAL
|
2.000.000
|
5.479
|
38.462
|
506
|
Para obtener la curva de n bombas en paralelo, para la misma altura manométrica, los caudales se suman. De manera analítica, siendo Q el caudal global, las curvas serían:
n
bombas iguales H = A + B(Q/n) + C(Q/n)2 h = D(Q/n) +E(Q/n)2
Considerando estas expresiones obtenemos las diferentes curvas para el funcionamiento de 1 bomba, 2 bombas o 3 bombas:
HB1
= 131+166Q – 8546Q2 HB2
= 131+ 83Q – 2136,5Q2 HB3
= 131+ 55,33Q – 946,56Q2
hB1
(%) = 2500·Q – 19500·Q2 hB2
(%) = 1250·Q – 4875·Q2 hB3
(%) = 833,3·Q – 2166,7·Q2
La curva de la conducción, la obtenemos a partir de la siguiente expresión, dado que las pérdidas de carga dependen del caudal: HC= Hg + hf
La
altura geométrica máxima de la impulsión es de 60 m. A partir de la
ecuación empírica de HAZEN-WILLIAMS para el PE, considerando que las pérdidas
de cargas singulares son un 10% de las continuas y diferenciando cada tramo de
tubería en función del timbraje obtenemos: HC60= 60+ 338,85·Q1,87
Nota: Las pérdidas de carga totales (hf) es la suma
de las pérdidas de carga continuas (hc) + las pérdidas de cargas singulares
(hs). Las pérdidas de carga continúas hc=J·L se pueden determinar a partir de
la ecuación empírica de HAZEN-WILLIAMS para el PE: J = 10,62·150-1,85·D-4,87·Q1,85
Por otro lado la altura geométrica mínima de la impulsión es de 47 m, y se produce cuando el nivel de la balsa de captación es máximo (cota 83) y el nivel de la balsa de regulación es mínimo (cota 130), por tanto en este caso la curva de la conducción será:
HC47= 47+ 338,85Q1,87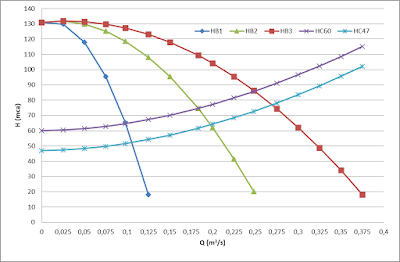 |
| Funcionamiento impulsión considerando el número de bombas en marcha a velocidad fija y el nivel de las balsas |
Del
cruce de las curvas de la conducción, en función de la altura geométrica, con
las curvas de las bombas obtenemos el rango de los puntos de funcionamiento de
la impulsión en función de los grupos de bombeo que estén en marcha y de la
diferencia de los niveles de las balsas. Sustituyendo en sus respectivas
ecuaciones obtenemos el rendimiento para cada caso.
1 BOMBA
|
2 BOMBAS
|
3 BOMBAS
|
||
Q(m3/s)
|
0,098
|
0,183
|
0,248
|
|
Q(m3/h)
|
353
|
659
|
893
|
|
HC60
|
H (mca)
|
65
|
75
|
86
|
h (%)
|
57,72
|
65,49
|
73,41
|
|
Q(m3/s)
|
0,106
|
0,198
|
0,270
|
|
Q(m3/h)
|
382
|
713
|
972
|
|
HC47
|
H (mca)
|
52
|
64
|
77
|
h (%)
|
45,9
|
56,38
|
67,05
|
Como se puede ver en la tabla anterior el rendimiento de las bombas, en condiciones normales de funcionamiento, va a variar entre el 45,9-73,41%, por tanto en muchas situaciones estaríamos fuera de la zona de rendimiento óptimo (65-70%).
Para conseguir que el funcionamiento de la bomba
se encuentre en su funcionamiento útil vamos a emplear el variador de
velocidad. Además con el variador de velocidad se puede
reducir la potencia absorbida por la bomba en los períodos de menor caudal, y también puede reducir el pico de intensidad en el arranque. Las
bombas mantienen un rendimiento aceptable mientras la velocidad se encuentra en
el intervalo del 60 al 100% de la nominal, disminuyendo considerablemente para
valores inferiores. El principal inconveniente de estos equipos es la
generación de armónicos (alteraciones en la red eléctrica). Para evitar que se
inyecten a la red, el variador está dotado de filtros.
Las curvas características
de una misma bomba a otro régimen de revoluciones se obtiene de: Hm = Aa2 + BaQ + CQ2 h = (D/a)Q0
+ (E/a2) Q2 a= n/n’
En nuestro caso las curvas
características en función de la velocidad de giro se obtienen de: HB1
= 131a2+166aQ –
8546Q2 hB1
(%) = (2500/a)·Q – (19500/a2)·Q2
En primer lugar vamos a
determinar el rango de caudales donde la bomba se encuentra dentro de la zona
de rendimiento óptimo. Despejando de la ecuación de rendimiento: hB1
(%) = 65 = 2500·Q – 19500·Q2
Obtenemos que el rango
de caudal estaría comprendido entre 0,036-0,092 m3/s. Sustituyendo en
la curva de la bomba obtenemos que las alturas manométricas estarían comprendidas
entre 126 – 74 mca. A partir de estos valores podemos calcular las curvas de
isorrendimiento: Hm = (Hm0/Q02)·
Q2 =k Q2
Por tanto en nuestro caso para un rendimiento del 65% obtendríamos:
Hm=(126/0,0362)·Q2 Hm= (74/0,0922)·Q2
En la siguiente figura se
muestra la zona de rendimiento óptimo cuando se encuentre en funcionamiento una
única bomba con velocidad variable. Como se puede observar la regulación del variador nos
va a permitir poder impulsar en condiciones de máximo rendimiento de la bomba.
 |
| Puntos de funcionamiento óptimo de una bomba a velocidad variable y nivel de las balsas |
90%
|
80%
|
70%
|
||
Q(m3/s)
|
0,080
|
0,059
|
0,029
|
|
Q(m3/h)
|
288
|
212
|
104
|
|
HC60
|
H (mca)
|
63
|
62
|
60
|
hb (%)
|
68,15
|
78,31
|
70,10
|
|
Q(m3/s)
|
0,072
|
0,051
|
||
Q(m3/h)
|
259
|
184
|
||
HC47
|
H (mca)
|
50
|
48
|
|
hb (%)
|
67,05
|
78,63
|
De igual modo cuando deban funcionar dos o tres grupos
de bombeo, se pondrá en marcha uno o dos de velocidad fija, y con el otro de
velocidad variable, de este modo pondremos conseguir que se trabaje en la zona
de máximo rendimiento.Para llevar a cabo un manejo adecuado de la estación de bombeo es necesario el empleo de indicadores de gestión. Un seguimiento energético periódico permita detectar anomalías, evitando que los equipos trabajen con bajas eficiencias energéticas durante un largo tiempo. Además con las Tecnologías de la Información y la Comunicación (TICs) podemos llevar un seguimiento de las instalaciones en tiempo real. El indicador energético más representativo es la energía específica (EacVs), que muestra la relación entre el consumo de energía y el volumen de agua. Otro indicador muy importante es el coste energético por unidad de agua (CENVs), y nuestro objetivo debe ser reducirlo al máximo.
A continuación vamos a calcular la energía específica (EacVs) para los diferentes puntos de funcionamiento de la instalación. La eficiencia del motor de los grupos de bombeo (hm) es del 95%. La potencia consumida por el motor (Nm) la podemos obtener de la siguiente ecuación: Nm = (g Q H) / hb hm donde g(N/m3) Q (m3/s) H (m) y N(W)
A continuación vamos a calcular la energía específica (EacVs) para los diferentes puntos de funcionamiento de la instalación. La eficiencia del motor de los grupos de bombeo (hm) es del 95%. La potencia consumida por el motor (Nm) la podemos obtener de la siguiente ecuación: Nm = (g Q H) / hb hm donde g(N/m3) Q (m3/s) H (m) y N(W)
EacVs en función de los grupos de bombeo a velocidad fija en marcha y nivel de las balsas
1 BOMBA
|
2 BOMBAS
|
3 BOMBAS
|
||
Q(m3/s)
|
0,098
|
0,183
|
0,248
|
|
Q(m3/h)
|
353
|
659
|
893
|
|
HC60
|
H (mca)
|
65
|
75
|
86
|
hb (%)
|
57,72
|
65,49
|
73,41
|
|
N(kW)
|
114
|
216
|
300
|
|
EacVs (kWh/m3)
|
0,323
|
0,328
|
0,336
|
|
Q(m3/s)
|
0,106
|
0,198
|
0,27
|
|
Q(m3/h)
|
382
|
713
|
972
|
|
HC47
|
H (mca)
|
52
|
64
|
77
|
hb (%)
|
45,9
|
56,38
|
67,05
|
|
N(kW)
|
124
|
232
|
320
|
|
EacVs (kWh/m3)
|
0,324
|
0,325
|
0,329
|
EacVs de una bomba a velocidad variable en función de la velocidad y el nivel de las balsas
90%
|
80%
|
70%
|
||
Q(m3/s)
|
0,08
|
0,059
|
0,029
|
|
Q(m3/h)
|
288
|
212
|
104
|
|
HC60
|
H (mca)
|
63
|
62
|
60
|
hb (%)
|
68,15
|
78,31
|
70,1
|
|
N(kW)
|
76
|
48
|
26
|
|
EacVs (kWh/m3)
|
0,265
|
0,227
|
0,246
|
|
Q(m3/s)
|
0,072
|
0,051
|
||
Q(m3/h)
|
259
|
184
|
||
HC47
|
H (mca)
|
50
|
48
|
|
hb (%)
|
67,05
|
78,63
|
||
N(kW)
|
55
|
32
|
||
EacVs (kWh/m3)
|
0,214
|
0,175
|
Comparando los valores de EacVs de las Tablas anteriores,
se obtiene que:
- El mayor consumo de energía específica es de 0,336 kWh/m3, y se produce cuando funcionan los tres grupos de bombeo a velocidad fija y la altura geométrica de la impulsión es máxima.
- El menor consumo de energía específica es de 0,175 kWh/m3, y se produce cuando funciona un grupo de bombeo al 70% de la velocidad nominal y la altura geométrica de la impulsión es mínima. En este caso el consumo de energía sería un 48% inferior al caso anterior.
Estos resultados ponen de manifiesto la importancia del manejo de la impulsión. Pudiéndose conseguir un gran ahorro energético:
REFERENCIAS:
- En función de los grupos de bombeo que estén en marcha.
- Cuando la velocidad de giro de una de las bombas es variable, y su valor se fija continuamente en base a los niveles de la balsas y el número de bombas que estén en marcha, para que las bombas trabajen en la zona de máximo rendimiento.
- Optimización del nivel de las balsas de tal modo que la altura geométrica de la impulsión sea la mínima requerida.
REFERENCIAS:
- Abadía, R., Rocamora, M.C., Ruiz, A., 2008. Protocolo de Auditoría Energética en Comunidades de Regantes. Volumen 10 de Eficiencia y Ahorro Energético. Agricultura Instituto para Diversificación y Ahorro de la Energía, IDAE.
- CENTER. 2014. CURSO “TECNOLOGÍA PARA ALCANZAR LA EFICIENCIA HÍDRICA Y ENERGÉTICA EN LOS REGADÍOS”.
- IDAE. 2005. Ahorro y Eficiencia Energética en Agricultura de Regadío. Instituto para Diversificación y Ahorro de la Energía, IDAE. Serie divulgación Ahorro y Eficiencia Energética en Agricultura 2.
- Martínez, V.; 2005. AMPLIACIÓN DE HIDRÁULICA E HIDROLOGÍA. Universidad Politécnica de Cartagena.
- Rocamora, M.C., Abadia, R., Ruiz, A. 2008. Ahorro y Eficiencia Energética en Comunidades de Regantes. Instituto para Diversificación y Ahorro de la Energía, IDAE. Serie divulgación Ahorro y Eficiencia Energética en Agricultura 9.
- Soto García M, Martínez Álvarez V, Martín Górriz, B. 2014. El regadío en la Región de Murcia. Caracterización y análisis mediante indicadores de gestión. SCRATS, 267 pp. http://repositorio.bib.upct.es/dspace/handle/10317/4069
- SIAR. 2009. Servicio Integral de Asesoramiento al Regante. Eficiencia energética en instalaciones de riego. Hoja 17. CREA. Universidad de Castilla La Mancha.
- UMH. Universidad Miguel Hernández. 2010. Curso de Gestor energético de Comunidades de Regantes. Instituto para Diversificación y Ahorro de la Energía, IDAE. FENACORE.


No hay comentarios:
Publicar un comentario